二叉树

存储结构

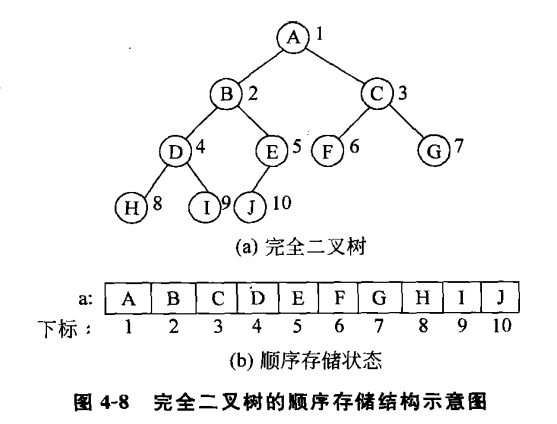
顺序存储结构

结言：递归算法简洁精练、可读性好、易理解,但其执行效率较低

非递归算法

用栈来实现

前序遍历(preoder traversal)

从二叉树的根结点开始，沿左子树一直深入到最左下结点时止，在深入的过程中访问所遇到的结点，并把所遇到结点的非空右孩子进栈；当左子树结点全部处理完之后，从栈顶退出当前最近访问过结点的右孩子，再按上述过程遍历该结点的右子树；如此重复，直到栈空时为止。

const preOrderTraversal = (root) => {
    if(root===null){
        return [];
    }
    let nodestack = [];
    let res = [];
    //根节点入栈
    nodestack.push(root);
    while(nodestack.length>0){
        //栈顶结点出栈
        let node = nodestack.pop();
        //进入结果集
        res.push(node.val);
        
        //右、左子树进栈
        if(node.right){
            nodestack.push(node.right);
        }
        if(node.left){
            nodestack.push(node.left);
        }
    }
    return res;
}

中序遍历(inorder traversal)

是沿左子树向下搜索的过程中先将所遇结点进栈，待遍历完左子树返回时从栈顶退出结点并访问，然后再遍历右子树。

const inOrderTraversal = (root) => {
    if (!root) {
        return [];
    }
    let res = [];
    let nodestack = [];
    while (root || nodestack.length) {
        while (root) {
            nodestack.push(root);
            root = root.left;
        }
        root = nodestack.pop();
        root.val && res.push(root.val);
        root = root.right
    }
    return res
}

后序遍历(postorder traversal)

当搜索指针指向一个结点时不能马上访问，需要先遍历左子树，所以结点需要进栈保存；

当遍历完左子树返回再次搜索到该结点时还不能进行访问，还需要遍历其右子树，所以结点需要再次进栈保存；

即一个结点在两次进栈两次出栈之后才能访问。为了区别某一结点指针的两次出栈,需设置一标志flag同结点同时进出栈，flag定义如下：

Continue...............

层次遍历(level-order traversal)

是从根结点开始访问，然后访问它的左孩子和右孩子，接下来是它左孩子的左孩子和右孩子，右孩子的左孩子和右孩子……

1. 首先将根节点入队列
2. 当队列不空，从队列中取出队头结点访问它，并在其左右孩子非空时，把它的左孩子和右孩子结点依次入队列
3. 反复执行(2),直到队列为空时止

const levelOrderTraversal = (root) => {
  let queue = [];
  let result = [];
  if (root !== null) {
    queue.push(root);
  }
  while(queue.length !== 0) {
    let level = [];
    let len = queue.length;
    for (var i = 0; i < len; i ++) {
      let currentNode = queue.shift();
      //访问每层结点
      level.push(currentNode.val);
        
      //下一层结点入队
      if (currentNode.left !== null) queue.push(currentNode.left);
      if (currentNode.right !== null) queue.push(currentNode.right);
    }
    //每层遍历结束
    result.push(level);
  }
  //返回一个二维数组
  return result;
}